Physique, lisible pour tous
Labo Prisme

À consulter avec le fureteur Firefox

Buts

• Se familiariser avec l’utilisation d’un goniomètre optique
• Constater que l’indice de réfraction dépend également de la couleur
• Modéliser cette variation selon la loi du baron Augustin Louis Cauchy

Matériel

• Goniomètre (aussi appelé spectroscope)
• Sources lumineuses: blanche pour la spectro et jaune pour éclairer la lecture du vernier
• Source d’alimentation
• Filtres de couleurs entre 450 et 690 nm

Montage

Théorie

Le montage et les mesures correspondent au numéro 2.4.9 (p.215) de Séguin:

La relation indiquée

est celle qui permettra de calculer l’indice $n$ pour chacune des longueurs d’onde que vous testerez.

NB: les prismes seront déjà placés comme dans l’exercice, tel que les angles de déviation $\delta$ seront minimaux ie: ils augmenteront si le prisme pivote dans un sens ou dans l’autre. Voir cette simulation très intéressante d’une prof à la retraite, G. Tulloue: Prisme ( draguez le prisme pour observer ce phénomène).

Mesures

La déviation angulaire $\delta =| \theta_1 - \theta_2 |$ s’obtiendra à partir de la position non-déviée $\theta_1$ mesurée seule une fois et de la position déviée $\theta_2$ mesurée pour chacune des couleurs des filtres distribués: 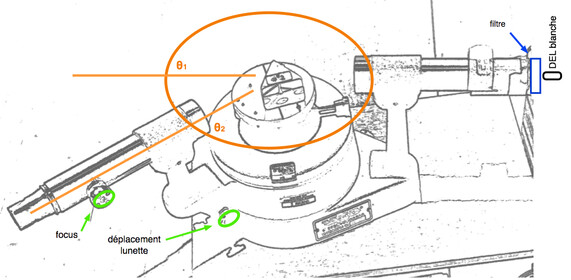Notez que le goniomètre est comme un rapporteur d’angle qui fait 360° et que la position de l’origine ($\theta = 0^{\circ}$) de ce rapporteur n’importe aucunement: seules les positions relatives des rayons sont pertinentes et mesurées, les écarts étant calculés par la suite.

Lecture du vernier

Cet appareil est l’un des plus précis du lab: il permet de déterminer la position le long du cercle avec une précision d’une partie dans 40 000 (et même 80 000 si on pousse la lecture aux demie-graduations!). Cette précision a un prix: la lecture est composée de multiples étapes, qui sont détaillées dans cette vidéo:

1. angle entier sur l’échelle du bas
2. demi degré ou non sur l’échelle du bas encore
3. minutes lues sur le vernier, graduations en haut.

Merci à la chaîne Youtube All Lab Experiments pour la figure (copiée sans permission…)

Manipulations

Le montage sera déjà complété, il ne restera qu’à faire les mesures de $\theta_2$ pour chaque couleur disponible. Les couleurs sont obtenues en filtrant la lumière émise par une DEL blanche (voir schéma plus haut à droite). Chaque équipe a un sac de filtres que vous vous échangerez durant le lab en conservant les filtres dans leur sac identifié. Il y a 26 filtres nommés de A à Z sur leur tranche. Manipulez-les toujours en les saisissant de côté sans toucher le verre de chaque face. Pour chaque filtre notez $\theta_2$ que vous obtenez en alignant la lunette sur la raie observée dans l’oculaire. Le réticule ne tue pas: centrez-le sur la raie en tournant la roulette de déplacement. Si la raie est floue, ajustez la mise au point avec le réglage du focus. Mesurez le plus de couleurs possibles, idéalement la totalité des 26 filtres… Chaque valeur d’angle est composée de trois données brutes qui doivent se retrouver dans votre cahier (dans la video: les 2 mesures main scale MS et celle vernier scale VS). Exemple:

Filtre	angle entier (MS)	demi-degré (MS)	vernier (VS)
A	269	30 min	17 min
Q	267	30 min	5 min
F	269	0 min	12 min
T	267	30 min	15 min

NB: Assurez-vous d’avoir les mesures des filtres turquoise E, jaune Q et rouge X

Mesures uniques

L’angle $\theta_1$ (c.-à-d, la position du rayon non-dévié, cf cette figure) doit être mesuré à la toute fin: appelez le prof ou le technicien pour vous assister. Notez également le numéro du prisme.

Traitement des données

Les calculs seront faits dans un tableur (avec les angles en radian!). Pour savoir quelle précision l’équation (1) précédente permet d’obtenir pour $n$, nous avons fait le calcul de propagation des erreurs pour vous et le résultat est:

Notez que les numérateurs $\frac{\Delta \alpha + \Delta \delta }{2}$ et $\frac{\Delta \alpha }{2}$ doivent être en radian.

Voici les longueurs d’ondes (± 1 nm) pour chaque filtre:

A: 450 nm; B: 467 nm; C: 470 nm; D: 480 nm; E: 488 nm; F: 500 nm; G: 500 nm; H: 505 nm; I: 515 nm; J: 520 nm; K: 532 nm; L: 540 nm; M: 546 nm; N: 550 nm; O: 568 nm; P: 580 nm; Q: 589 nm; R: 600 nm; S: 610 nm; T: 620 nm; U: 632 nm; V: 640 nm; W: 650 nm; X: 656 nm; Y: 671 nm; Z: 690 nm;

Voici les angles au sommet $\alpha$ pour chaque prisme:

#1: 60°46min; #2: 60°40min; #3: 59°17min; #4: 60°9min; #5: 59°52min; #6: 59°53min; #7: 60°42min; #8: 59°58min; #9: 59°59min; #10: 60°6min; #11: 60°2min.

Ces angles au sommet ont été mesurés avec minutie et possèdent une incertitude de $\Delta \alpha = \pm 0.5 \,min$ .

Travail demandé

• le détail du calcul de $\frac{\Delta n}{n}$
• un graphique $n(\lambda)$, qui devrait ressembler à ceux de la page 209
• un graphique linéarisé qui permet d’ajuster une droite et en déterminer les deux premiers coefficients de la loi de Cauchy, A et B (avec une incertitude déterminée par la méthode min-max pour ceux-ci)
• un tableau indiquant les valeurs obtenues des coefficients de Cauchy, de valeurs similaires à celles inscrites à cette page Wikipedia
• évaluez le pouvoir de dispersion $\omega$ de votre prisme avec les filtres E, Q et X selon
  $$\omega =\frac{n_{turquoise\,E} - n_{rouge\, X}}{n_{jaune\, Q}} \approx \frac{\delta_{turquoise\,E} - \delta_{rouge\, X}}{\delta_{jaune\, Q}}$$

  que l’on peut interpréter comme le ratio de la largeur de l’arc-en-ciel sur sa position.

Questions supplémentaires

Q1

Si vous disposiez d’un second prisme, fait avec le même matériau que celui que vous venez d’étudier, mais avec un angle au sommet beaucoup plus petit, par exemple 10 ̊, lesquelles des quantités suivantes seraient différentes de celles de votre prisme ?

1. la position angulaire de la raie rouge.
2. l’angle de déviation minimum pour la raie rouge.
3. l’indice de réfraction pour la raie rouge.
4. le pouvoir de dispersion.
5. les constantes de la relation de Cauchy

Q2

Quelle différence concrète y aurait-il entre deux prismes équilatéraux de même indice pour le filtre jaune Q, mais dont les valeurs du pouvoir de dispersion seraient 1% et 5% ?